Units-and-measurements Cheat Sheet
Vectors in 2D and 3D
A vector
Component Form
- 2D:
- 3D:
Magnitude of a Vector
- 2D:
- 3D:
Unit Vector
A unit vector
Vector Addition and Subtraction
If
- Addition:
- Subtraction:
Graphically, vector addition follows the parallelogram or triangle rule.
Scalar (Dot) Product
Here,
- If
, then and are perpendicular (unless one is a null vector).
Vector (Cross) Product (3D only)
Magnitude:
- If
, then and are parallel (unless one is a null vector). -
-
-
Position, Displacement, Velocity, and Acceleration
Position Vector
Describes the location of an object in space from the origin.
Displacement Vector
Change in position from an initial point
Average Velocity
Instantaneous Velocity
The time derivative of the position vector.
Speed is the magnitude of the velocity vector:
Average Acceleration
Instantaneous Acceleration
The time derivative of the velocity vector (second derivative of position).
Motion with Constant Acceleration
If
Equations of motion can be applied independently to each component.
Equations of motion can be applied independently to each component.
- Velocity:
- Position:
Where
Component-wise Equations (2D example)
| X-component | Y-component |
|
|
|
|
|
|
|
|
|
Projectile Motion
Motion of an object under gravity only (neglecting air resistance).
- Acceleration:
(assuming y-axis is vertical upwards) -
Initial velocity:
Where
Where
Equations of Motion
-
(constant) -
-
-
Key Formulas (assuming
- Time to Max Height
- Maximum Height
- Time of Flight (
): For landing at - Horizontal Range
: For landing at - Trajectory Equation:
Uniform Circular Motion (UCM)
Motion in a circle at constant speed
- Radius of circle:
- Angular speed:
(radians/second) - Period:
(time for one revolution) - Frequency:
Centripetal Acceleration (
Directed towards the center of the circle, changes the direction of velocity, not its magnitude.
In vector form:
Centripetal Force (
The net force causing centripetal acceleration.
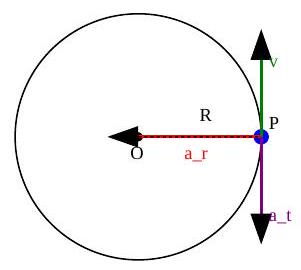
Non-Uniform Circular Motion
Speed is not constant, so there is both tangential and radial acceleration.
- Tangential Acceleration
: Changes the speed of the object. It's parallel or anti-parallel to the velocity vector.
- Radial (Centripetal) Acceleration (
): Changes the direction of the object. Directed towards the center.
- Total Acceleration (a): Vector sum of tangential and radial accelerations.
Relative Motion
Velocity of object A relative to object B :
Velocity of object B relative to object A :
If
General relative velocity equation:
General relative velocity equation:
Where
Example: Boat in a River
-
: velocity of Boat relative to Water -
: velocity of Water relative to Ground (river current) -
: velocity of Boat relative to Ground
Example: Airplane with Wind
-
: velocity of Airplane relative to Air -
: velocity of Air (wind) relative to Ground -
: velocity of Airplane relative to Ground
Newton's Laws of Motion
Newton's First Law (Law of Inertia)
An object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force.
Newton's Second Law
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. The direction of the acceleration is in the direction of the net force.
Where
Newton's Third Law
For every action, there is an equal and opposite reaction. If object A exerts a force
Common Forces
Weight (
Force of gravity exerted by a planet on an object.
Where
Normal Force (
The force exerted by a surface perpendicular to the surface, preventing an object from passing through it.
Example: For an object on a horizontal surface,
Example: For an object on a horizontal surface,
Tension (
The force transmitted through a string, rope, cable, or wire when it is pulled tight by forces acting from opposite ends.
Friction Force (
Force that opposes relative motion or attempted motion between surfaces in contact.
- Static Friction (
): Opposes impending motion. It adjusts its magnitude up to a maximum value.
- Kinetic Friction (
): Opposes actual motion. It is generally constant once motion starts.
Where
Spring Force (Hooke's Law)
The force exerted by an ideal spring, proportional to its displacement from equilibrium.
Where
Applications of Newton's Laws
Free-Body Diagrams (FBDs)
A diagram showing all external forces acting on an object. Essential for solving force problems.
- Isolate the object(s) of interest.
- Draw all forces acting on the object (not forces exerted by the object).
- Choose a coordinate system.
- Resolve forces into components.
- Apply Newton's Second Law (
).
Connected Objects
Treat each object separately with its own FBD. Identify common forces (e.g., tension in a string, normal force between contacting surfaces) and common accelerations.
Atwood Machine
Two masses connected by a string over a pulley.
Assumptions: massless string, massless and frictionless pulley.
Assumptions: massless string, massless and frictionless pulley.
Inclined Plane
Object on a ramp. Resolve gravity into components parallel and perpendicular to the incline.
- Perpendicular component:
(balanced by normal force) - Parallel component:
(causes motion down the incline)
Work, Energy, and Power
Work Done by a Constant Force
Where
Work Done by a Variable Force (1D)
Work Done by a Variable Force (1D)
Kinetic Energy (
Energy due to motion.
Work-Energy Theorem
The net work done on an object equals the change in its kinetic energy.
Gravitational Potential Energy (
Energy due to an object's position in a gravitational field.
Where
Elastic Potential Energy (
Energy stored in a spring or elastic material.
Where
Conservative Forces
Forces for which the work done is independent of the path taken (e.g., gravity, spring force). Associated with potential energy.
Non-Conservative Forces
Forces for which the work done depends on the path taken (e.g., friction, air resistance). Dissipate mechanical energy.
Conservation of Mechanical Energy
If only conservative forces do work, total mechanical energy (
Conservation of Energy with Non-Conservative Forces
If non-conservative forces like friction are present, they do work (
Power (
The rate at which work is done or energy is transferred.
Units: Watts (W), where
Momentum and Collisions
Linear Momentum (
A vector quantity, product of mass and velocity.
Units:
Impulse (
Change in momentum. It's the integral of force over time.
For a constant force:
Impulse-Momentum Theorem
The impulse acting on an object equals the change in its momentum.
Conservation of Linear Momentum
If the net external force on a system of objects is zero, the total linear momentum of the system remains constant.
For a two-body collision:
Types of Collisions
- Elastic Collisions: Both momentum and kinetic energy are conserved.
- Inelastic Collisions: Momentum is conserved, but kinetic energy is NOT conserved (some is lost to heat, sound, deformation).
- Perfectly Inelastic Collisions: Momentum is conserved, objects stick together after collision (
). Maximum possible kinetic energy loss.
Coefficient of Restitution
A measure of the elasticity of a collision (1D).
-
for perfectly elastic collisions. -
for perfectly inelastic collisions. -
for inelastic collisions.
Center of Mass (CM)
The average position of all the mass in a system.
For discrete masses:
For discrete masses:
Velocity of CM:
The total momentum of a system is equal to the total mass times the velocity of its center of mass.
If
If
Rotational Motion
Angular Position (
Measured in radians, angle from a reference line.
Angular Displacement (
Change in angular position.
Angular Velocity (
Rate of change of angular position.
Units: rad/s.
Angular Acceleration (
Rate of change of angular velocity.
Units:
Rotational Kinematics (Constant Angular Acceleration)
Tangential and Angular Quantities Relationship
For a point at radius
- Arc length:
- Tangential speed:
- Tangential acceleration:
Note: These apply when
Moment of Inertia (I)
Rotational equivalent of mass. Measures resistance to angular acceleration.
For a point mass
For a system of discrete masses:
For continuous mass distribution:
For a point mass
For a system of discrete masses:
For continuous mass distribution:
Parallel-Axis Theorem
Used to find moment of inertia about an axis parallel to one through the center of mass.
Where
Rotational Kinetic Energy (
Torque (
Rotational equivalent of force. Causes angular acceleration.
Magnitude:
Newton's Second Law for Rotation
Work Done by Torque
For constant torque:
Rotational Power
Angular Momentum (
Rotational equivalent of linear momentum.
For a point particle:
Magnitude:
For a point particle:
Magnitude:
Conservation of Angular Momentum
If the net external torque on a system is zero, the total angular momentum of the system remains constant.
For a rigid body:
Gravitation
Newton's Law of Universal Gravitation
Attractive force between any two objects with mass.
Where
Gravitational Field Strength
Acceleration due to gravity at a distance
On Earth's surface,
Gravitational Potential Energy (
For two masses
Escape Speed (
Minimum speed an object needs to escape the gravitational pull of a celestial body.
Where
Orbital Speed (
Speed required for a stable circular orbit at radius
Kepler's Laws of Planetary Motion
- Law of Orbits: All planets move in elliptical orbits with the Sun at one focus.
- Law of Areas: A line that connects a planet to the Sun sweeps out equal areas in equal times. This is a consequence of conservation of angular momentum.
- Law of Periods: The square of the orbital period (
) of a planet is proportional to the cube of the semi-major axis of its orbit. For circular orbits, .
Simple Harmonic Motion (SHM)
Periodic motion where the restoring force is directly proportional to the displacement from equilibrium and acts in the opposite direction.
Key Parameters
- Amplitude (
): Maximum displacement from equilibrium. - Period (T): Time for one complete oscillation.
- Frequency (
): Number of oscillations per unit time. . - Angular Frequency
.
Position, Velocity, Acceleration (for
- Position:
- Velocity:
- Acceleration:
Mass-Spring System
Angular frequency:
Period:
Simple Pendulum
For small angles
Angular frequency:
Angular frequency:
Period:
Where
Energy in SHM
Total mechanical energy (
At maximum displacement (
At equilibrium
Thus,
At equilibrium
Thus,